数学動画教材1102_01「テーマ：数の大小を不等号で表すことができる」について

１．◆ はじめに ◆

今回は、数学動画教材1102_01「テーマ：数の大小を不等号で表すことができる」の内容について少し詳しく説明します。

中学校数学を学ぶ人が動画教材を見てからノートにまとめるときに参考になるような内容を目指すとともに、教える人の目線でも参考になるように考えて記事を書いたつもりです。いずれも２πｒ（にーぱいあーる）の見解でしかないのですが、よかったら参考にしてください。

また、この動画教材を使った自分なりの勉強の仕方で迷っているときは、ブログ｢動画教材を使った勉強の仕方｣を参考にしてください。サイト内検索で探す場合は、カテゴリー「勉強の仕方」で検索するとすぐ見つかります。アーカイブ（月単位）ならば「2018 ６月」で検索してください。

 

1102_01_数の大小を不等号で表すことができる_説明

1102_01_数の大小を不等号で表すことができる_練習問題

２．◆ このテーマで一番大切なこと ◆

日本語も英語も、世界中の言葉すべてには主語と動詞があります。中学１年生にはすこし難しいかもしれませんが、簡単に言うと、｢わたしは｣「あなたは」などの言葉が主語で、「～する」「～している」などを意味する言葉が動詞です。
主語だけでは、その人が何をするのか伝わりません。動詞だけでは、誰がやっていることなのか伝わりません。このように相手に何かを伝えるときは必ず「主語と動詞がセット」になっています。
実は数学も、日本語や英語とほとんど変わらない言葉なのです。なぜならば、数学も考えたことを人に伝える道具だからです。
このテーマで一番大切なことは、不等号を使って正の数・負の数の大小関係を人に伝えることができるということです。そして、そのために不等号を「動詞」と考える発想が大切だと２πｒ（にーぱいあーる）は考えています。

３．◆ 次に大切なこと ◆

次に大切なことは、日本語や英語と同じように、数学も同じことを伝えるのにいろいろな表現方法があるということです。つまり、答えがひとつでないこともあるということを理解することです。
例えば、「５は３より大きい」は、「３は５より小さい」と表現しても、その大小関係は同じように人に伝わります。注目している主語が、５なのか３なのかというだけのことです。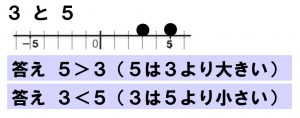
数学では、「５は３より大きい」を「５＞３」、「３は５より小さい」を「３＜５」と表現するので、どちらを答えても正しいということになります。
日本語がわかる人は、必ず数学もわかるということですね。

ちなみに、この不等号は英語の動詞と使い方がよく似ています。そこら辺は、英語をもっと勉強するとわかるようになります。

以上のことから、不等号の問題では「他に答えはないかな？」と考える癖をつけてください。

◆ ３つ以上の数の大小 ◆

３つ以上の数の大小を表すときは、説明動画で示したことで十分です。日本語がわかればまず大丈夫でしょう。

でも、ひとつだけ確認したいことがあります。それは、

「－３＜０＜４ と ４＞０＞－３ を数直線で考えるとどうなるかわかりますか？」ということです。・・・以外に難しいでしょ？

この答えは、「目盛りのつき方が逆の数直線」を思い浮かべるとわかってきます。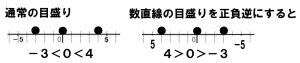

説明はしないので、数直線をよく見てください。

 

４．◆ 最後に ～ ｘを使った不等式 ◆

最後に、数直線を使って大小関係を考えるとき、知っておいてほしいことを紹介します。それは「数字をグループで考えることもある」ということです。

練習問題動画の問題１(1) にｘを使った問題があります。ここでのｘは、その状況にあった数全部を表しています。

例えば ｘ＜２ を考えてみると、この式は「ｘは２より小さい数のグループ全部を表している」と考えます。このことを、数直線で考えると図のようになります。この図では、ｘの範囲を矢印で表していますが、数直線を太線にしてｘの範囲を表すこともあります。

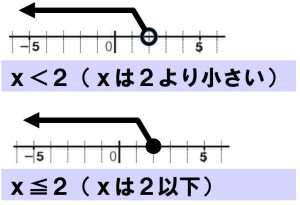そして、押さえておきたいことは、＞ と ≧ の表現の違いです。ｘの範囲に２が入らないときは＞、２が入るときは≦をつかいます。

ちなみに、不等号を使った式を「不等式」と呼びます。この不等式の関係を数直線で表すときは、「＞ や ＜  は白丸、 ≧ や ≦ は黒丸 を使う」ことになっています。

また、 ｘ＜２と同じ大小関係を表している２＞ｘは「２はｘより大きい」と表現しますが、個人的には『ｘを主語にして「ｘは２より小さい」と表現することが多い』ように感じています。そこで、動画教材（練習問題）ではあえて「ｘを主語にすることが多い」と書いておきました。

1102_01練習問題１(5)です。

 

今回は、以上です。

追記

ｘ≦２は「ｘは２以下」と表現することが多いですが、慣れるまでは常に「ｘは２より小さいかまたは等しい」という正確な表現を使うと、意味をはっきり理解できるのでお勧めです。