数学動画教材1101_01「テーマ：数直線の性質が理解できる」について

１．◆ はじめに ◆

今回は、数学動画教材1101_01「テーマ：数直線の性質が理解できる」の内容について少し詳しく説明します。

中学校数学を学ぶ人が動画教材を見てからノートにまとめるときに参考になるような内容を目指すとともに、教える人の目線でも参考になるように考えて記事を書いたつもりです。いずれも２πｒ（にーぱいあーる）の見解でしかないのですが、よかったら参考にしてください。

また、この動画教材を使った自分なりの勉強の仕方で迷っているときは、ブログ｢動画教材を使った勉強の仕方｣を参考にしてください。サイト内検索で探す場合は、カテゴリー「勉強の仕方」で検索するとすぐ見つかります。アーカイブ（月単位）ならば「2018 ６月」で検索してください。

 

1101_01_数直線の性質が理解できる_説明

1101_01_数直線の性質が理解できる_練習問題

２．◆ このテーマで一番大切なこと ◆

小学校で考えた数直線は、０から出発して右側に伸びていました。では、０より左側に直線を伸ばすとどんな数になるのだろう？ といった発想で生まれた数が「負の数」であることを、なんとなくでもよいので、理解できることが一番大切です。

そのことを、この動画教材では「数直線は、無数の数字が大きさの順に並んでできた直線」と表現しています。そして、「０より小さい数を負の数を呼ぶ」、「負の数は記号－（マイナス）をつけて表すことにした」とつながっていくのです。あとは、負の数同士の大きさを判断できたり、用語になれればこのテーマはＯＫです。

数学が苦手な人は、分数や小数がでてきたり、よくわからない用語がでてくると、そこらへんに引っかかってしまいがちです。言い換えると、「数直線は、無数の数字が大きさの順に並んでできた直線」という数直線の性質が「考えるよりどころ」であることを忘れてしまいがちです。・・・大切なことは理解できているのに、目の前の問題をそこから出発して考えることを忘れたがために「わからない」と感じてしまうことも多いのではないかと、２πｒ（にーぱいあーる）は考えています。

練習問題の動画教材では、どの問題も「数直線は、無数の数字が大きさの順に並んでできた直線」をよりどころにして説明できます。具体例をあげて後で説明します。

３．◆ 次に大切なこと ◆

次に大切なことは「用語」です。慣れないうちは、いろいろな用語がごちゃごちゃになるものです。それは当然のことです。用語をすぐ理解していつでも使えるようになるわけがありません。でも、先に話したように、数直線の性質を思い浮かべてそこから考えるようにすると、自然と用語が身についてきます。

人間は繰り返さないと、覚えたり、うまく使いこなすことができません。まして忘れるのは当たり前です。ところが、いつも数直線の性質を思い浮かべて考えるようにすると、数直線を軸に自然といろいろなことを繰り返し思い出すことになり、結局いろんな内容とつながって用語を覚えることができるようになります。一石二鳥ですね。

こうしたことからも、練習問題動画は数直線を思い浮かべてから考える習慣を身につけてください。

４．◆ 数直線の性質を思い出してから考えるとは？ ◆

数直線をよりどころにした考え方の例を、動画教材の練習問題を例にいくつか紹介します。いままでの文章を読んでイメージできなかった人も、きっとイメージできるようになると思います。

練習問題動画　問題２

整数は数直線上の太い目盛りの数字（青い丸で囲んだ場所）とイメージしておけば、小数や分数はその間の数と、セットでイメージできます。小数や分数をもっと詳しく調べようと考えたときも数直線から考えることができますが、今回はテーマからそれるので省略します。

 

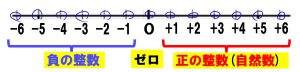
また、「自然数には０が入らない」と覚えるよりも、「整数は負の整数と０（原点）と正の整数（自然数）」とセットで覚えるようにすると効果的です。また、正の数・負の数といったら数直線上のすべての数、つまり「青い丸で囲んだ目盛りの数字以外も全部」とイメージすればよいのです。

たったこれだけのことを意識して考えるだけでも、今回のテーマに関する用語は確実に身につきます。

練習問題動画　問題３

これは、温度計をイメージして考えている人が多いのではないでしょうか。この温度計も数直線です。数直線が縦になったものと考えればいいのです。そして、数直線の正の数・負の数が「０より大きい数」、「０より小さい数」であったことと同じに、温度計では単位も考えて「０℃より高い温度」、「０℃より低い温度」ととらえればよいのです。

練習問題動画　問題５

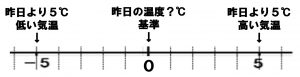
(1) この問題は、数直線の基準である０が昨日の気温と考えることに気づくことが大切です。そこに気づけば、目盛り－５は「昨日より５℃低い気温」を表すことがわかります。

(2) は「支出＝マイナス、収入＝プラス」といたってシンプルなのですが、実は数直線で考えるには難しい内容です。

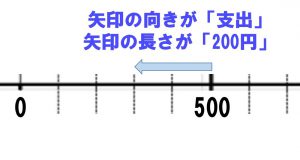
「目盛り－２００が２００円の支出」、「目盛り＋３００が３００円の収入」と考えることもできますが、２πｒ（にーぱいあーる）は違うとらえ方をしています。それは「支出と収入は矢印で考える」ということです。別ないい方をすると、「動きのあるものは矢印で考える」ということです。

負の方向に向く矢印は「減る＝支出」を表し、正の方向に向く矢印は「増える＝収入」と考えるのです。このように考えると、原点０を基準にしなくても考えることができるようになります。

「５００円持っている人が、２００円の支出をした」・・・数直線でイメージできるでしょ？

 

練習問題の説明で「対義語を＋－で表すこともある」と表現しましたが、このようなイメージを持って頭を整理してもらうといいのかなと思います。

 

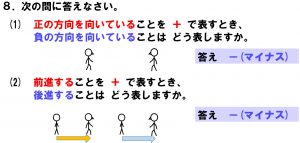
そして、このことを意識して載せた問題が、問題８です。

(1)は「正の方向を向く＝プラス」、「負の方向を向く＝マイナス」

(2)は「前進する＝プラス」、「後進する＝マイナス」と考えるわけですが、

(2) は矢印であることに注意します。つまり、(1) は状態を表すのに対して、(2) は動きを表すことに気づいてほしい問題なのです。

問題５(2) で、支出、収入を矢印でイメージしたのは、この対義語が「お金の動き」を表していたからです。このように「動きを表すのは矢印」ととらえるといろいろな事柄を数直線で考えやすくなります。　（もちろん自分なりに別な理由をつけてイメージしてもかまいません。とにかくすべてがうまく説明できればよいのです。）

話はそれますが、数学が好きな人や得意になる人は「この問題を数直線で考えるとどうなるんだろう？」と、自分で自分に質問して考える人だと思います。このようなことに興味を持って自分で考えたり、調べたりするようになると数学の力はグングン伸びていきます。知らないうちに用語やその使い方を繰り返し思い浮かべることで覚える効果もあるでしょうが、きっと、考える楽しさを少しずつ感じることができるからだと思います。みなさんも、ゆっくりでいいので「何をイメージして考えを始めようかな？」という気持ちを大切にしてみてください。

練習問題動画　問題７

これは「同じ性質を、＋－と対義語を使って表す」ことを理解してもらうための問題です。ここが、今回のテーマで一番難しい内容です。中学１年生でこの問題の考え方を頭で完全に整理することは普通できません。もしできたあなたは、天才に近いと２πｒ（にーぱいあーる）は思います。では説明します。

(1) を数直線で考えるとこんな感じになります。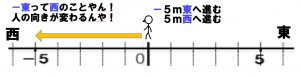

この問題で、状態は「東に向く」です。動きは「進む」です。「進む」をそのままにして考えると、「－東」はどんな状態を表すでしょう。・・・そう「西に向く」です。つまり、「－東＝西」と考えて「－５ｍ東に進む」は「５ｍ西に進む」と同じと考えるのです。そして、「５ｍ西に進む」でも正解ですが、＋－の符号になれてほしいので問題に合わせて「＋５ｍ西に進む」を解答にしました。

実は、解答はもうひとつあります。

この問題で、状態は「東に向く」です。動きは「進む」です。「東に向く」をそのままにして考えると、「－進む」はどんな動きを表すでしょう。・・・そう「後ろ向きに進む（後退する）」です。だから「－５ｍ東に進む」は「５ｍ東に後退する」となります。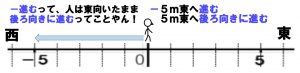

どうでしょう。「状態」と「動き」を考えて、マイナスはどちらにかかるのかと考えると、答えは２種類あることがわかりますね。ここまで整理して考えられた人が、「考え方を頭で完全に整理」できた人です。このことを自分一人で考えられた人は本当にすごいです。

さて、ここまで理解できれば　問題７の(2)、(3) は簡単です。

(2) は、「状態」を表す言葉がありません。つまり「動き」だけを考えればよいのです。

「＋ひく」って他にどう表すんだろう？

「－たす」だ。

じゃあ答えは「－５をたす」だろう。・・・と考えていけばよいのです。　(3) は同じなので省略しますね。

このように考えていくことが、正負の数の加法（たし算）での重要ポイントのひとつである「ひき算はたし算に直せる」ということの理解につながります。

練習問題動画　問題９

この問題を「ただ用語を覚えているかどうかを聞く問題」と考えるのは間違いです。この問題も問題２と同様に「数直線を使って習ったことを整理する問題」と考えましょう。

ここではこれ以上説明しません。自分の力で問題９を数直線を使って考えてみてください。

５．◆ おわりに ◆

「負の数はなぜ生まれたの？」、「どのように考えて生まれたの？」・・・と考える人はあまり多くはないでしょう。気になっても余裕がないのでパスという人も多いでしょう。

２πｒ（にーぱいあーる）も余裕がなかったのでパスしていました。まあ、ある程度イメージを持っておきたいと思ってはいましたが・・・　そんな２πｒ（にーぱいあーる）が持っている数学の歴史に対するイメージを紹介します。根拠も乏しく、どってことない内容なので、パスしてもらってかまいません　(^^;

—————————————-

数学の歴史は、新しい数を発見する歴史。人間の歴史の最初まで遡ると、「指折り数えることができる自然数」を最初に人は使ったはず。そして、「分け合うことから生まれた分数や小数」、「インドで発見されたという０」、「０より小さい数を考えて生み出された負の数」・・・という具合に数が発見されてきた。
中学３年生で「同じ数を２回かけて２になる数」を考える。これは「平方根」というそれまでは扱ってこなかった数。円周率π（パイ）＝3.1415･･･は分数の形では表すことが無理な数であることが知られてた。そして、平方根も分数の形では表すことが無理だと発見（証明）されていた。そこで、これらをまとめて「無理数」と呼ぶことにした。中学校ではここまでの数を扱う。ちなみに、無の反対は有なので、無理数に対して有理数ということばが生まれたと勝手に思っている。

高校に行くと「２乗して負の数になる数」を考える。その名前は「虚数」、虚数に対して今までの数全体を「実数」と呼ぶ。この実数と虚数の和の形で表される数字を「複素数」と呼ぶ。このような数字があるおかげで難しい計算も答えを出すことができるようになった。

これらは別な見方ができる。「５÷３の答えが出るようにしたい」→「小数1.666の発明、分数5/3の発明」、「１－３の答えが出るようにしたい」→「－２の発明」、「２乗して２になる数を見つけたい」→「平方根ルート２の発明」・・・と考えると、「数学の歴史は、難しい計算をするために新しい数を発明してきた歴史」とも考えられる。本当は、こっちのほうが正しいような気がする。

—————————————-

この内容を年表にしたいと考えたこともありましたが、いまだにやる気がおきません (^_^;)

以上です。