数学動画教材1111_01「テーマ：正負の数における乗法の意味が理解できる」について

◆ はじめに ◆

中学校数学を学ぶ人が、動画教材を見てからノートにまとめるときに参考になるような内容を目指すとともに、教える人の目線でも参考になるように考えて記事を書いたつもりです。いずれも２πｒ（にーぱいあーる）の見解でしかないのですが、よかったら参考にしてください。

また、この動画教材を使った自分なりの勉強の仕方で迷っているときは、ブログ｢動画教材を使った勉強の仕方｣を参考にしてください。サイト内検索で探す場合は、カテゴリー「勉強の仕方」で検索するとすぐ見つかります。アーカイブ（月単位）ならば「2018 ６月」で検索してください。

動画教材へのリンク　1111_01_正負の数における乗法の意味が理解できる_説明_by_２πｒ（にーぱいあーる）

動画教材へのリンク　1111_01_正負の数における乗法の意味が理解できる_練習問題_by_２πｒ（にーぱいあーる）

 

◆ 乗法・乗法の意味 ◆

今回のテーマのねらいは、「乗法・除法の意味を理解すること」です。

本来、乗法と除法は切っても切れない関係にありますから、乗法と除法の意味を自分なりに納得して理解できることが最も大切なこととなります。（今は、細かいことにはこだわらなくてもよいです）

ちなみに、説明動画の最後の方で突然「積（せき）」という用語を使っています。話の流れから想像できた人もいるかと思いますが、積は「乗法の答え」のことです。加法の答え、減法の答え、乗法の答え、除法の答えをそれぞれ、和、差、積、商といいます。ここは動画教材に載せることを忘れてしまいました (^_^;)

２πｒ（にーぱいあーる）は、乗法と除法の関係を次のように考えています。

– – – – – – – – – – – – – –

３×２＝６は誰もが知っていますから、

「３×◇＝６のとき、◇はいくつ？」と聞かれたとき、「２です。」と誰もが答えることができます。

では、「１１×◇＝１２３のとき、◇はいくつ？」と聞かれたらどうでしょう？

すぐ答えられる人は少ないのではないでしょうか。

そこで、誰もがすぐ◇を求められる方法を考えました。その方法が除法（わり算）です。

つまり、３×２＝６だから３×◇＝６のときの◇を求めるために「６わる３（６÷３）」という計算をすればよいと考えたのです。

つまり、◇を求めるために生まれたのが除法ということになります。

ここで、「１１×◇＝１２３のとき、◇はいくつ？」に戻ると、

◇＝１２３÷１１＝１３と計算できるので、誰もが「◇は１３です」と答えられるようになるということです。

– – – – – – – – – – – – – –

このような関係は、加法と減法にもいえます。

つまり、「２＋◇＝５」の◇を求めるために生まれたのが減法というこです。

これらのことは小学校でも触れられていると思いますが、どうでしょう？

ちなみに、

「７×◇＝３のとき、◇はいくつ？」と聞かれたら、

「◇＝３÷７＝３／７ です。」と答えることになりますが、

当然、分数という数がなかったら、

誰かが分数をつくっただろうと簡単に想像できる・・・

などと考えていくと、少しは身近に感じませんか ？

・・・無理かもですね (^^ゞ

※ 確かめ　７×３／７＝３　ＯＫ！

 

◆ 「負の数をかける」意味 ◆

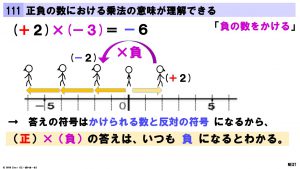
動画教材では、「負の数をかける」とは「向きを変える」ことだと説明しています。

このことをもう少し詳しく説明します。

実は、（＋２）×（－３）＝－（２×３） は 次のような式がより正確に意味を表しています。

（＋２）×（－３）＝（＋２）×（－１）×３

つまり、「かけるマイナス３」とは「マイナス１をかけて３倍すること」と考えるのです。

そうすると、「マイナス１をかけること」が「向きを変えること」を表しているとわかります。

ですから、正確には「マイナス１をかけることが向きを変えることを表している」ということなのです。

では、

（＋２）×（－３）＝－（２×３） と表したのは何故かというと、

「符号を先に決めて、後は小学校のかけ算をすればいい」ことを理解してほしかったからです。

このように、式にはそれぞれに意味があるので、式の意味をしっかり理解してください。

 

◆ 約分の仕方 ◆

約分の仕方は知っていても、

小学校でわり算が苦手だった人は、答えが分数の形になってから約分を考える人が多いように感じています。

きっと頑張って身につけたのだと思いますが、中学生になったら「途中計算の段階で約分」をしてください。

このやり方が絶対に計算が楽です！

中学校では分数の分母分子が大きな数になることも多いので、最後に約分をすると 、約分もしにくく、ミスも多くなります。

そして、一番理想的なのは「途中計算の段階で約分して、最後にさらに約分できないか確かめる」という姿勢を持つことなのです。

ですから、いまのうちに途中計算の段階で約分ができるようになりましょう。

もちろん、「答えの符号を先に決める」を確実に身につけることが最も大切です！

今回は、以上です。