数学動画教材1105_01「テーマ：加法の素早い計算方法が理解できる」について

◆ はじめに ◆

今回は、数学動画教材1105_01「テーマ：加法の素早い計算方法が理解できる」の内容について少し詳しく説明します。

中学校数学を学ぶ人が動画教材を見てからノートにまとめるときに参考になるような内容を目指すとともに、教える人の目線でも参考になるように考えて記事を書いたつもりです。いずれも２πｒ（にーぱいあーる）の見解でしかないのですが、よかったら参考にしてください。

また、この動画教材を使った自分なりの勉強の仕方で迷っているときは、ブログ｢動画教材を使った勉強の仕方｣を参考にしてください。サイト内検索で探す場合は、カテゴリー「勉強の仕方」で検索するとすぐ見つかります。アーカイブ（月単位）ならば「2018 ６月」で検索してください。

 

動画教材へのリンク　1105_01_加法の素早い計算方法が理解できる_説明_by_２πｒ（にーぱいあーる）

動画教材へのリンク　1105_01_加法の素早い計算方法が理解できる_練習問題_by_２πｒ（にーぱいあーる）

◆ 最も大切なことは２つ  ◆

今回のテーマで最も大切なことは、「自信を持って、一番最初に答えの符号を決めることができる」ということです。「一番最初に」がポイントです！

中学校では、たし算やかけ算のような基本的な計算では「最初に答えの符号を決める」ことに慣れる必要があります。正の数・負の数を学んだわけですから、答えもプラスかマイナスのどちらかになります。（０になることもたまにありますが）　「その答えの符号が先にわかれば、あとはなんとかなる」という感覚をぜひ身につけてください 。必ず、計算に慣れれば慣れるほど、このことが大切だとわかってきます。

最も大切なことは、実はもうひとつあります。それは「注意深さ」です。

慣れてくると「うっかり、減法なのに加法に直さずに同符号・異符号の２数の和を使って計算してしまう」ミスがよく見られます。せっかく理解して、覚えて、使えるようになっても、この最初の段階でミスをすることが意外に多いのです。また、これはとてももったいない話です。

ですから、常に「減法だったら加法に直す」という気持ちを持って問題を見るようにしてください。練習問題動画教材は、そのことに気づいて欲しいと考えて制作されています。ポイントは「一番最初よりも最初に」です。

どうでしょう？　練習問題を見て、「もし減法だったら、まず加法に直さないと！」という気持ちで問題を見ていましたか？

最初からこのことを意識していた人は、「なかなかセンスあり」です ＼(^_^)／

 

◆ 加法は４つのパターンで考える ◆

答えの符号を決める考え方ですが、説明動画で説明してある通りです。この動画での説明は、正の数・負の数の加法を４つのパターンに分けて数直線で考えるのですが、実は、「負の数　たす　正の数」、「正の数　たす　負の数」、「負の数　たす　負の数」の３つのパターンしか説明していません。

なぜかわかりますか？

それは、「正の数　たす　正の数」は小学校でやってきたパターンだから説明するまでもないと考えたからです。その点も理解したうえで、しっかり読み込み、練習問題に取り組むと理解しやすくなります。

では、３つのパターンについて簡単な解説をつけておきます。

※厳密に考えるともう少しパターンは多くなるのですが、そこら辺は、興味のある人が自分で考えてみてください (^_-)v　・・・もちろん、結論は同じになります。

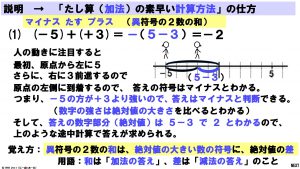
１枚目の説明 (1) は、「負の数　たす　正の数」で「負の数の絶対値の方が大きい場合」、つまり「負の方向に動く距離の方が大きい場合」を考えています。

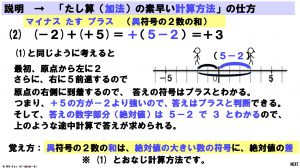
２枚目の説明 (2) は、「負の数　たす　正の数」で「正の数の絶対値の方が大きい場合」、つまり「正の方向に動く距離の方が大きい場合」を考えています。

(1) も (2) も、「異符号の２数の和」ということになります。どちらも、答えの符号は最終的に到着した場所の符号ですから、「答えの符号は、絶対値の大きい方の数の符号と同じになる」ことがわかります。

このことを、「異符号の２数の和は、絶対値の大きい方の符号が答えの符号になる」とまとめて表現します。

そして、答えの数字部分（絶対値）は、(1) と (2) の図からわかるように「２数の絶対値の差」となります。ちなみに、差とは「大きい数　ひく　小さい数　の答え」のことで、結局は「小学校のひき算の答え」のことです。

以上のことから、答えの符号と答えの絶対値の求め方をできるだけ短い文章で表すと、

「異符号の２数の和は、絶対値の大きい方の数の符号に、絶対値の差をつければ求められる」

となります。数学が苦手ではない人は、数直線の図とこの文章を、計算をするたびに思い起こしてなれてください。数学が苦手な人は・・・。

 

◆ 数学が苦手な人は、どうやって数学の文章になれればいい？ ◆

少し話がそれますが、２πｒ（にーぱいあーる）は、数学は「母国語の力が重要な学問」だと考えています。なぜならば、数式や数学独特の言葉遣いを理解する前には必ず、頭の中で毎日使っていることばで自分なりの表現をしているはずだと思うからです。もちろん、図や式でイメージが浮かんでいる人もいるはずですが、まったく母国語を使わずに考えている人はいるのでしょうか？

２πｒ（にーぱいあーる）は、特殊な人を除いて、いないと考えています。

話をもとに戻します。

数学が苦手な人は、「異符号の２数の和は、絶対値の大きい方の数の符号に、絶対値の差をつければ求められる」をどうやって身につければよいのでしょう？

２πｒ（にーぱいあーる）は、「まず、自分なりのことばで表現」してみることが大切だと思います。たとえば、

「符号の違う２つの数のたし算の答えは、答えの符号は数字部分の大きい方の符号になるから、それを一番最初に考える。そして、答えの数字部分は２つの数の数字部分をひき算して求める」

といった表現にしてみるのです。練習問題の途中計算を書くとき、この文章を繰り返し思い出しながら考え方に慣れることが、「理解の第一歩」です。

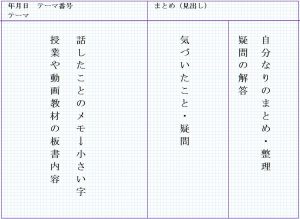この文章は、少々長くてもかまいません。自分なりのことばで、できれば、自分が大切だと思うポイントをいれながらまとめることが大切です。この場合は、「・・・それを一番最初に考える。そして・・・」が自分が大切だというポイントです。ちなみに、こういったことを書き込むノートの場所は、右ページの「気づいたこと」や「自分なりのまとめ」のどちらかに、自分の決めたルールにしたがって書き込みましょう。

このように、自分なりの表現で考え方を理解してから、「異符号の２数の和は、絶対値の大きい方の数の符号に、絶対値の差をつければ求められる」という数学的な文章に最終的になれればよいのです。

日本人は国語を大切にしましょう。自分の考えたことを自分と他人に伝える大切なアイテムですから。

 

そういえば、３つのパターンについて簡単な解説をしていましたね。

３つ目のパターンの解説に戻ります。

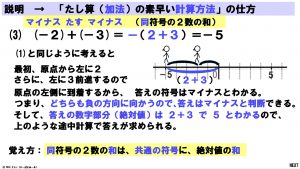
３枚目の説明 (3) は、「負の数　たす　負の数」の場合です。この場合の答えの符号は、「負の方向に行って、さらに負の方向に行く」わけですから、必ず答えは負になることがわかります。

答えの絶対値は、２つの数の絶対値をたした距離だけ動くので、「２つの数の絶対値の和」となります。

スライドでは説明していませんが、「正の数　たす　正の数」つまり小学校でやってきたたし算も、｢答えの符号は、２つの数に共通な符号プラス｣、「答えの絶対値は、２つの数の絶対値の和」のように、文章でまとめることができます。

以上のことから、同符号の２数のたし算の答えは、「同符号の２数の和は、共通の符号に、絶対値の和で求められる」という文章でひとまとめにすることができます。

まとめのスライドにある文章が、最終的なまとめの文章になります。この文章が必要な場面ですぐ思い浮かび、数直線や途中計算が書けるようになってください。

 

 

---

２つの数の和の求め方

　「異符号の２数の和は、絶対値の大きい方の数の符号に、絶対値の差」

　「同符号の２数の和は、共通の符号に、絶対値の和」

　　で求められる！

---

 

 

◆ 練習問題動画で注意すべきこと ◆

あとは、「再確認」とあるスライドの通り、(1) ならば「異符号だ→答えの符号はマイナスだ→答えの数字は絶対値の差だ」のように考えて答えを出してください。

何度も繰り返しますが、最初に答えの符号を考えてください。そして、それよりも前に「加法であることを確認」してください。減法だったら必ず加法に直して計算することをセットで意識して、練習に取り組みましょう。

 

以上のことをまとめると、スライドにあるような表現になります。もちろん「加法かどうか確認することを忘れずに！」がポイントですね。

 

今回は、以上です。