数学動画教材1104_01「テーマ：ひき算はたし算に直せることが理解できる」について

◆ はじめに ◆

今回は、数学動画教材1104_01「テーマ：ひき算はたし算に直せることが理解できる」の内容について少し詳しく説明します。

中学校を学ぶ人が動画教材を見てからノートにまとめるときに参考になるような内容を目指すとともに、教える人の目線でも参考になるように考えて記事を書いたつもりです。いずれも２πｒ（にーぱいあーる）の見解でしかないのですが、よかったら参考にしてください。

また、この動画教材を使った自分なりの勉強の仕方で迷っているときは、ブログ｢動画教材を使った勉強の仕方｣を参考にしてください。サイト内検索で探す場合は、カテゴリー「勉強の仕方」で検索するとすぐ見つかります。アーカイブ（月単位）ならば「2018 ６月」で検索してください。

 

動画教材へのリンク　1104_01_ひき算はたし算に直せることが理解できる_説明_by_２πｒ（にーぱいあーる）

動画教材へのリンク　1104_01_ひき算はたし算に直せることが理解できる_練習問題_by_２πｒ（にーぱいあーる）

◆ 中学校数学を理解する第一歩  ◆

今回のテーマでは、数直線上を歩く人をイメージして「顔の向きを考えると、同じ動きが２種類ある」ことを理解できることが最も重要となります。そのためには、今まで考えてきたことすべてが理解できていることが大切です。

このような理由から、このテーマを理解することが、中学校数学を理解する第一歩だと考えてください。

最初のスライドに「復習（もっとも大切）」とタイトルされているのは、このような意図があります。復習のためのスライドは、３枚用意しました。

３枚目のスライドは、前回のテーマの内容をまとめている図ですが、もし「たし算とひき算が同じ動きをしている」ことに気づいていたあなたは、なかなかよいセンスを持っています。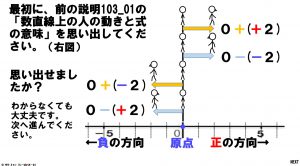

それこそが、「たし算はひき算に直せる」し、逆にいえば「ひき算はたし算に直せる」ということを示していることになるからです。このあたりの説明は、動画教材を見てもらえれば十分だと思います。

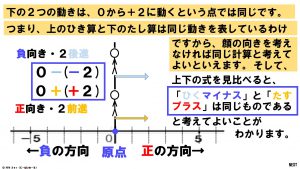そして、そんな便利な性質があるなら、「ひき算はすべてたし算に直してから計算しよう」となったわけです。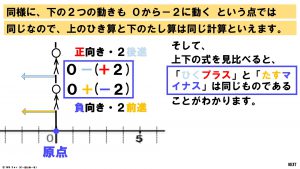

※ これからは、たし算は「加法」、ひき算は「減法」という専門用語を使います。

「減法は加法に直す」ことになった理由は、３つ考えられます。

①　「加法を素早く計算する方法がある」から。

②　加法と減法が混じった計算は、加法だけにして計算した方が「楽をするための工夫ができる」から。

③　加法の記号 ＋（たす）を省略する書き方「項を並べた式が発明された」から。

これら３つについては、別な場所で詳しく説明します。

①は、次の動画教材のテーマです。「同符号の２数の和、異符号の２数の和」という計算方法ですが、２πｒ（にーぱいあーる）は簡単に「同符号の和・異符号の和」ということがあります。

②については、別なテーマで触れます。「加法の交換法則」、「加法の結合法則」というルールをうまく使うことで計算が簡単になることもあるという内容です。

③については「発明された」と表現しましたが、誰がいつ決め、どのように広がったのかについては全くわかりません。根拠がありませんので、２πｒ（にーぱいあーる）が勝手に想像したと考えてもらって結構です。ただ、このように説明すると「項を並べた式」が理解されやすいと考えています。「項を並べた式」についても別なテーマで詳しく触れます。

 

◆ ルールは覚え方が大切 ◆

加法を減法に直すルールは、「ひくマイナス」は「たすプラス」に、「ひくプラス」は「たすマイナス」に、それぞれ変えてよいというルールです。このルールは、図で理解してから覚えることが大切です。そして、できるだけ短い文章で覚えた方が楽ができます。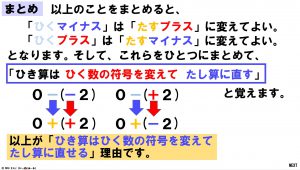

このように考えて、スライドにあるように「ひき算は、ひく数の符号を変えてたし算に直す」と覚えてください。

『「ひくマイナス」は「たすプラス」に直す、「ひくプラス」は「たすマイナス」に直す』という２つの場合を短い文章で表しているから楽というだけでなく、短い文章で記憶すると「頭の中が整理されてくる」からです。

人に教えるときは、『「ひくマイナス」は「たすプラス」に直す、「ひくプラス」は「たすマイナス」に直す』と説明した方がよい場合があります。

頭の中では短い文章で記憶して、説明するときは、やさしい表現を使うことができる・・・ここまでできるようになって、「人に教えるくらい理解できた」といえると思います。

後は、スライドにある通り「中学校ではひき算はたし算に直して計算」しますから、スラスラと直せるように練習に取り組んでください。

ここは「練習あるのみ！」です。

 

今回は、以上です。