数学動画教材1103_01「テーマ：正負の符号、たし算とひき算の意味が理解できる（数直線）」について

◆ はじめに ◆

今回は、数学動画教材1103_01「テーマ：正負の符号、たし算とひき算の意味が理解できる（数直線）」の内容について少し詳しく説明します。

中学校数学を学ぶ人が動画教材を見てからノートにまとめるときに参考になるような内容を目指すとともに、教える人の目線でも参考になるように考えて記事を書いたつもりです。いずれも２πｒ（にーぱいあーる）の見解でしかないのですが、よかったら参考にしてください。

また、この動画教材を使った自分なりの勉強の仕方で迷っているときは、ブログ｢動画教材を使った勉強の仕方｣を参考にしてください。サイト内検索で探す場合は、カテゴリー「勉強の仕方」で検索するとすぐ見つかります。アーカイブ（月単位）ならば「2018 ６月」で検索してください。

 

動画教材へのリンク　1103_01_正負の符号、たし算とひき算の意味が理解できる（数直線）_説明_by_２πｒ（にーぱいあーる）

動画教材へのリンク　1103_01_正負の符号、たし算とひき算の意味が理解できる（数直線）_練習問題_by_２πｒ（にーぱいあーる）

◆ たし算、ひき算の意味 ◆

３＋１＝４ は「３たす１は４です」という意味ですが、大きさを考えると「３より１つ大きな数字は４です」という意味にもなると理解できます。このことを数直線で考えれば、「３を出発して右に１進むと４に着く」となります。
また、３－１＝２ は「３ひく１は２です」という意味ですが、大きさを考えると「３より１つ小さな数字は２です」という意味にもなります。数直線で考えれば、「３を出発して左に１進むと２に着く」となります。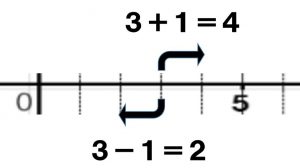
つまり、「たし算は数直線上を右に進むこと」、「ひき算は数直線上を左に進むこと」となります。これらは、小学生でも理解できる基本的な説明の仕方だと思います。
普通はこれで納得してしまうのですが、２πｒ（にーぱいあーる）はここに落とし穴があると考えていました。
「納得しやすいがために、数直線上を人が動くときの顔の向きにまで目を向けることがなくなったのではないか？」ということです。それが、しいては「減法が加法になることが記憶に残らない原因」につながっているのではないかと考えていました。

◆ 顔の向きを考えると・・・ ◆

では、顔の向きを考えるとどうなるのでしょう？
顔の向きは、「正の方向」または「負の方向」を向く２通りあります。当然、「正の方向を向くことを＋（プラス）」と決めれば、｢負の方向を向くのは－（マイナス）｣となります。
となれば、数直線上を動く人を考えるとき、すべての場合は４通りあることになります。
この４通りの見つけ方が、説明スライドの最後「◆ 頭をよくするテクニック」です。
表の 例、２番目、３番目、４番目 は、それぞれが最初のスライドの 例、２番目の解答、３番目の解答、４番目の解答 を表しています。
この動画教材を１～２回見てこのことが理解できていれば、あなたはなかなかのものです。自信を持っていいと思います。

 

◆ 正負の符号、たし算とひき算の意味 ◆

こうして、正負の符号、たし算とひき算の意味を理解する準備が整いました。
ここまでのことを自分で気づいてもらいたいと、問いかけた質問が最初のスライドです。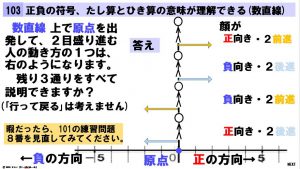
もちろん時間も短いですから気づかないのが普通です。よく説明を見て理解できればそれでＯＫです。
でも、最初のスライドを見て「ピン」ときた人は、頭の柔らかさを見せた人だと思います。いわゆる数学的センスがある人かもしれません (^_^)v

数学だけではありませんが、当たり前と思われていることを別な角度から見て考えることを続けると、頭というものはよくなってくるのだと思います。（もちろん、記憶力とは別です）

話はそれてしまいますが、次元という言葉を知っていますか？
０次元は点、１次元は直線、２次元は平面、３次元は空間、４次元は空間と時間・・・というふうに２πｒ（にーぱいあーる）は認識していますが、５次元、６次元・・・と広げたり、－１次元、－２次元・・・を考えたり、0.5次元などの小数次元を考えたりする発想（妄想？）が大切だと思います。
それがあるかないか、正しいか正しくないか、は後でわかることです。そして、正しい理由を冷静に考えていく姿勢が大切だと思います。
数学は、考えたことを記述するためにある言語ですから、数学の言葉で考えたことを組み立てていくことが「冷静に考える」ことになります。
今、知られていることの多くは、一般の人は考えても見なかったことを、じっくりゆっくり冷静に考え続けたり、ときにはパッとひらめいて、うまく現実に合っていることを冷静に確かめて世界に広まったものです。
昔の人は「地球は丸い」などと考えていなかったことを知っていますか？ 現代の人にとってそんなことは幼児の考えだと笑う人もいるかもしれませんが、それが常識だった時代もあったことを考えると、「もし・・・だったら」という発想はとても大切なものだと思いませんか？
ちなみに、物理の世界では、次元は１１次元まで議論されているようですが、その詳細は２πｒ（にーぱいあーる）には理解できません。しかし、最先端の物理学で、１０次元だ、１１次元だ、と議論されて、どうやら１１次元らしいというところまで来ているということが重要です。なぜなら、このことから「自由に発想することの大切さ」を ２πｒ（にーぱいあーる）は改めて感じるからです。
まぁ、２πｒ（にーぱいあーる）的には「次元は無限にある」方がしっくりくるのですが・・・もちろん、直感ですけど (^^ゞ

話を元に戻しますね。

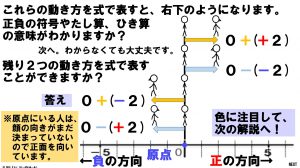正負の符号、たし算、ひき算の意味がわかったところで、実際の計算と結びつけているのが、２枚目、３枚目のスライドです。
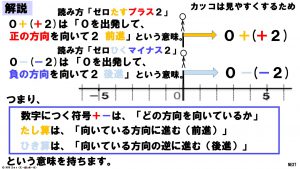ここで注意してもらいたいのは、「０を出発して」という条件です。

何ごとも基本が大切ですから、「０を出発して」という条件で最初は考えてほしいということです。
そして、このときの「０からの距離」を「絶対値」と呼びます。絶対値は、正負の数の符号を取った数字部分と考えてもＯＫです。この用語は、後で学ぶ 1105_01_正の数・負の数【加法の素早い計算方法が理解できる】で使われるので、ここで軽く紹介しています。
また、ここが理解できれば「減法がなぜ加法に直せるのか」を理解できます。自分なりに考えをまとめて次のテーマに臨んでもらうと、すばらしいなと思います。
あとは、特に説明することはありません。スライドをよく見てください。

 

◆ ０を出発しない場合 ◆

「０を出発して」考えることになれたら、次の段階は「０以外を出発して」計算することを考えてみます。その説明部分が、説明動画の後ろから２枚目のスライドです。
ここでの考え方のポイントは、ただの３という数字は「０＋３」と考えてよい、３＋２という計算は「０＋３＋２」と考えてよいということです。
こう考えると、正負の数の加法・減法すべてが「０を出発して」考えることができるようになります。
３＋２＋１のように数字が増えても同じ考え方で理解することができます。
どんな加法・減法も数直線上にいる人の動きで表すことができるなんで、すごいことだと思いませんか？ つまり、人の動きを式だけで言い表すことができるということですよ。それも、とても短い表現で・・・
３＋２＋１を日本語で説明すると、「人は正の方向を向いて、０を出発して３進んだ。次に３を出発して２進んだ。さらにその場所から１進んだ。」と、まるでゲームの勇者の動きの説明ような、長い文書になってしまいます。でも、数式なら「３＋２＋１」だけでＯＫです。

この「式は物事を簡単に表すことができる」ということが、実は数学が生き残ってきた大きな理由です。日本語や英語で詳しく説明すると膨大な文書量になる内容でも、とても簡単に表現することができるということは、難しいことを考えれば考えるほど、数学のよさが身にしみるようになるということですから。
尤も、その分、一般の人には理解しにくくなる傾向はありますが、それは、日本語や英語で記述しても同じことですから、やはり数学の言語としても能力は高いのかと思います (^_^)v

また、脱線してしまいました。済みません (^^ゞ

ここでの内容も、後で学ぶ 1105_01_正の数・負の数【加法の素早い計算方法が理解できる】で使われます。
数学では、すべての内容が次の内容を考える基礎になります。だからこそ、数学は最初の基本をしっかり理解する必要があります。油断せずに、練習問題をすらすら解けるだけでなく、「ここはこう考えてこうなるんだ」と説明できるようになってください。

 

◆ おまけ　加法の教え方はいろいろあるけど・・・ ◆

以上で、このテーマで書きたいことは終わります。
いろいろ脱線したので、脱線ついでに数学を教える人を対象に、２πｒ（にーぱいあーる）の考えていることを少し紹介します。
興味がなければ、ここはこれで終わってもらって結構です。

加法（たし算）の教え方はいろいろあります。
① 数直線上で、「たす」が右へ進む、「ひく」が左へ進む、であることを理由に教える。
② ○をプラス、●をマイナスと考え、視覚的に捉えさせて、教える。
③ トランプの得点をプラス、減点をマイナスとして、教える。
などなど・・・
しかし、このように加法だけに重きを置いて教えることに疑問を感じていました。

中学校では、「数直線 → 数の大小 → 加法 → 減法」のような順序で加法・減法を教えることが多いと、経験的に感じています。
２πｒ（にーぱいあーる）も現役時代はほぼこの順序で教えてきました。しかし、この順序で教えると、どうしても「減法が加法に直せる理由」を印象に残せないと感じていました。
生徒にとっては、減法が加法に直せることをとにかく覚えて、加法で学んだ「同符号の和、異符号の和」を使ってスラスラ計算できるようになればよいわけですから、「なぜ、減法は加法に直せるのか？」なんて、生徒にとってはどうでもよいことになってしまうということです。
実際、「減法を加法に直す手順」や「同符号・異符号の２数の和」を覚えることに精力を注ぎ、覚えた頃には「減法が加法に直せる理由」なんで遠い過去のことになり、ましてや「なぜ？」と考える余裕なんてない生徒がほとんどだと思います。みなさんはどう感じていますか ？

このようなことから、そもそもの原因は加法・減法の教え方にあるのかもしれないと考えたのです。つまり、加法と減法を一緒に理解できればしっかり印象に残せるのではと考えて、できあがったのが今回の103_01動画教材です。

※ 数直線を使う「加法の教え方①」は、103_01の教え方に似ていますが、動く人の向きを考えていないので全くの別物ですので明確に区別してください。

103_01の教え方は以前から頭にあったので、たまに授業の流れの中で使えそうな部分を使って教えることもありました。しかし、最初から授業を組み直して授業時数内にうまく納められるか、期待通りに加法・減法を同時に理解してもらえるか、多忙な中で時間をつくり出せるか、といったことを考えると、なかなか踏み切れないでいたのです。

もし、この教材を使って教えてくれる方がいて、いろいろご意見をいただければ、より使える教材に成長するかもしれません。単元全体の流し方を自分なりに消化できる方は、よかったら取り入れてみてください。

また、向きを意識した考え方は実はとても重要です。中学生にはまだ早いですが、向きを考えることで数式の意味を視覚的に理解できることもよくあります。
後で出てきますが、負の数をかけるとは「向きを変える」という意味を持ちます。図で考えると「数直線上の矢印の向きを１８０°変える」ということになります。

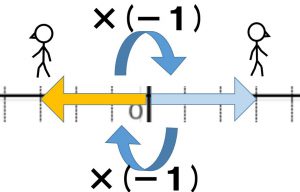以前、「同じ数字を２回かけると－１になる数」つまり「虚数」という数を高校で習うとお話ししました。この虚数を１つかけるとは「数直線上の向きを９０°回転する」と解釈すると理解しやすくなります。虚数に虚数をかけるとは、９０°回転して、また９０°回転することになりますから、結局１８０°回転したことになります。つまり－１をかけたことと同じになるという感じです。
このように、難しい数学を考えるときにイメージをつかむためにも方向を意識した理解はとても重要です。

今回は、以上です。