数学動画教材1204_01「テーマ：ａ＋５とａ＋５ａの違いが理解できる_同類項の加法計算」について

◆ はじめに ◆

中学校数学を学ぶ人が、動画教材を見てからノートにまとめるときに参考になるような内容を目指すとともに、教える人の目線でも参考になるように考えて記事を書いたつもりです。いずれも２πｒ（にーぱいあーる）の見解でしかないのですが、よかったら参考にしてください。

また、この動画教材を使った自分なりの勉強の仕方で迷っているときは、ブログ｢動画教材を使った勉強の仕方｣を参考にしてください。サイト内検索で探す場合は、カテゴリー「勉強の仕方」で検索するとすぐ見つかります。アーカイブ（月単位）ならば「2018 ６月」で検索してください。

動画教材へのリンク　1204_01_ａ＋５とａ＋５ａの違いが理解できる_同類項の加法計算_説明_by_２πｒ（にーぱいあーる）

動画教材へのリンク　1204_01_ａ＋５とａ＋５ａの違いが理解できる_同類項の加法計算_練習問題_by_２πｒ（にーぱいあーる）

◆ わからなくなる理由 ◆

今回の動画教材における内容は、２πｒ（にーぱいあーる）が中学校数学教師時代に経験したことがもとになっています。

この経験を動画教材に取り入れたのは、このテーマのような課題を示して班で話しあわせたらホワイトボードに書かれていた班の意見の大半がブログに載せたような予想を超えたものだったので、自分の教え方を振り返るよいきっかけになったことを覚えていたからです。

いろいろなご意見もあるとは思いますが、「こんな考えで間違えることもあるんだ」程度に受け取ってもらえれば幸いです。

大切なことは、基本をしっかり身につけていないと思わぬ勘違いをするということです。その勘違いがさらに別な勘違いや、「わからない」という気持ちを生むといういうことです。そして、間違え方を理解することが学びに役立つということです。

当たり前のことのようですが、勘違いがいつどこで発生するのか、一番大きな影響を与える勘違いはいつ起きるのかという議論はそれほどなされていないように思います。

まぁ、議論していたとしてもよい方法はなかなか見つからないと思いますが・・・ (^_^;)

２πｒ（にーぱいあーる）は、最も影響のある勘違いがこのテーマで起きていると考えています。そして、小学校で学んだ内容や、正の数・負の数で学んだ内容をあいまいなままにしている人たちが授業内容が進んでいくときにちょうどこのあたりで自信や興味を失っていくのではないかと考えています。

つまり、２つの要素がこのあたりで重なることが「中学校数学がわからなくなる最も大きい理由」ではないかと考えています。

みなさんは、どう思いますか？

※ この件に関するご意見はこのブログのコメント欄にお願いします。

◆ やっぱり基本が大切 ◆

みなさんは、これまで学習してきた内容のうち何割身についたと思いますか？

５割？、６割？、７割？、８割？、９割？、それとも完璧？

２πｒ（にーぱいあーる）は、８割以上身につけていないとだんだんわからなくなってくる危険性が高いと感じています。

５割未満の人は５割を、５割の人は６割を、６割の人は７割を、７割の人は８割を、８割の人は９割を、９割の人は完璧を目指してください。

学んだその日の基本をその日のうちに理解して、できるだけ早くその内容をすぐ思い出せるようになる努力をするような積み重ねが大切です。

いろいろなことを話してきましたが、やっぱり基本が大切なのです。

◆ 基本と基礎の違い ◆

ところで、２πｒ（にーぱいあーる）は、基本と基礎の違いを次のように考えています。

基本問題とはいいますが、基礎問題というと何か違和感があります。

つまり、その問題を理解すればいろいろな問題を解く参考になるものを基本問題というのではないでしょうか。（動画教材では「例」や「例題」といっていますが・・・）

それに対して、いろいろな基本問題を理解して使えるようになると「基礎ができた」というような使い方をするように思うのです。そして、それとは別に用語などは基礎と呼ぶのかなと・・・

つまり、学ぶ過程で最初に必要な問題や考え方を「基本」、用語などを「基礎」といい、その基礎・基本がある程度身についたらまとめて「基礎」というのではないかと考えています。

このとき、「基礎」でなく「基礎・基本」といってもいいわけですから、基礎と基本の区別がつかなくなってきて「どう使ってもいんじゃない？」、「基礎も基本も同じでしょ？」といった感じになったのではないかと推測しています (^_^)v

数学では、学んだことを使って次の問題を解決していきます。ですから、小学校１年生のいろいろな算数の基礎や基本が身について、それを基礎として小学校２年生の算数の基本を学んできたのです。これを積み重ねることでみなさんは小学校の算数を終わらせてきたはずです。そして、その基礎をもとに中学校数学を学び始めているのが今なのです。

「昨日のテーマで学んだ基本は次のテーマの基礎」となります。もちろん、昨日のテーマで用語などが加わっていれば「昨日のテーマで学んだ基礎・基本は今日のテーマの基礎」となります。

「正の数・負の数の単元で学んだ基礎・基本は、次に学ぶ文字式の基礎」となります。「中学１年生で学んだ基礎・基本は中学２年生の数学を学ぶための基礎」となります。

本当に数学は積み重ねの学問だと思います。

ちなみに、基本と基礎についてインターネットで調べたら、２πｒ（にーぱいあーる）は「！スッキリ」というサイトの内容が一番しっくりくると感じました。興味のある人は覗いてみてください。

URL：https://gimon-sukkiri.jp/basic/

◆ バケツの穴と学力 ◆

このように考えると、今まで学んできた基礎が土台となって新しい基本を学ぶのですから、基礎はとても大切だとわかってもらえると思います。基礎がなければ学力はつきません。

２πｒ（にーぱいあーる）は、このことを踏まえて学力をバケツの水に例えて説明することが多かったです。

バケツに蛇口から水を入れることを想像してみてください。

蛇口は、先生、教科書、問題集、動画教材、ノート、ときには友人です。

この蛇口から基礎・基本という水をもらってためていくと学力がついたという感じになります。

ところが、バケツの底に穴が開いているとしたら･･･

水はなかなかたまりませんね。つまり、基礎・基本が流れ出ていくので学力がつきにくいということになります。

中学校数学の場合、バケツの底は「小学校の基礎」です。

たし算、ひき算、かけ算、わり算のスピードが遅かったり間違いが多い人は、水は底からちょろちょろと流れ出ています。これでは数学を理解するのに、つまり水がたまるのに時間がかかってしまいます。

かけ算、わり算がよくわかっていない人は、水は底から勢いよく流れ出ています。もっと時間がかかってしまいます。もしかしたら、水は減ってしまいます。

たし算、ひき算、かけ算、わり算がよくわかっていない人は、水は底からさらに激しい勢いで流れ出ています。これでは、水がたまるはずがありません。つまり、学力はつきません。

どうでしょう？

バケツの穴をふさぐことがとても大切だとわかりましたか？

小学校で学んだことが大切だとわかりましたか？

前の時間に学んだことが大切だとわかりましたか？

数学がわかるようになるためには、今まで学んだことを理解してすぐ出てくるようにすることが重要です。

また、小学校の基礎がある程度身についている人でも、中学校で学ぶ内容が十分に身につかないとバケツの壁に穴が開いている状態と同じになりますから、学力が上がりにくくなってきます。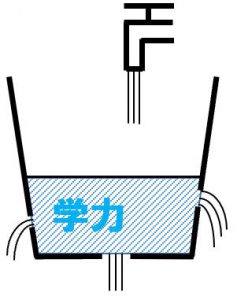

バケツの壁は学んだことを身につけた中学校の基礎・基本といえます。しっかりした壁をつくるには、よく考えて理解したり、何度も練習してすぐ答えられるようにしたり、暗記すべき用語はしっかり暗記することが大切なのです。

いままでも何度も繰り返してきましたが、ひとつひとつのテーマを確実に身につける努力が最も重要です。

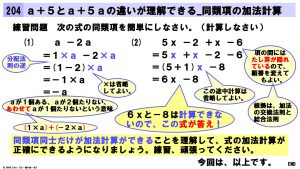説明動画の最後のスライドに今まで学んできた内容をいろいろ吹き出しでつけておきました。いままでの基礎がどの程度固まっているのかを確認してみてください。

今回は、以上です。